At equilibrium, [R] + [D] ⇔ [RD] → Biological response....................(2)
Such that the affinity constant KA = [RD]/ [D][R]. This is the same equation as that derived from Langmuir’s saturation isotherm, which derives from the law of mass action. It is possible to describe the occupancy theory in the following way:
- The receptor/drug (RD) complex is reversible
- Receptor/drug (RD) association is a bimolecular process
- Receptor/drug (RD) dissociation is a monomolecular process
- All receptors of a given type are equivalent and behave independently of one another
- The concentration of a drug is greatly in excess of the receptor and therefore the binding of the drug to the receptor does not alter the free (F) concentration of the drug.
- The response elicited by receptor occupation is directly proportional to the number of receptors occupied by the ligand
The equilibrium dissociation constant Kd gives a measure of the affinity of the drug for the receptor.
Kd = ([R][D])/[RD]....................................(3)
Kd can also be defined by the two micro constants for rate on and off k+1 (forward rate constant) and k–1 (reverse rate constant) so
that Kd = k–1/k+1, where Kd is the concentration of the drug (D) that occupies 50% of the available receptors.
When a receptor is occupied by an agonist, the resulting conformational change is only the first of many steps usually required to produce a pharmacologic response. The transduction process between occupancy of receptors and drug response is often termed coupling. The relative efficiency of occupancy-response coupling is partially determined by the initial conformational change in the receptor—thus, the effects of full agonists can be considered more efficiently coupled to receptor occupancy than can the effects of partial agonists. Coupling efficiency is also determined by the biochemical events that transduce receptor occupancy into the cellular response.
Biological responses/effects can be derived from the following equation with respect to the drug-receptor occupancy.
[R] EF/EM = [RD]/[R]T...........................................(4)
Where EF is the fractional response, EM is the maximal response,
[RD] is the concentration of receptor-drug complex and [R]T is the total receptor concentration.
At equilibrium, Kd = [R][D]/[RD] So, [RD]= [R][D]/Kd. putting the [RD] value in equation-4,
EF= EM. [D]/ (Kd + [D])...........................(5)
When the occupancy assumption is true, a half-maximal effect is observed when [D] is equal to Kd of the drug-receptor interaction.
2. Two-state receptor theory
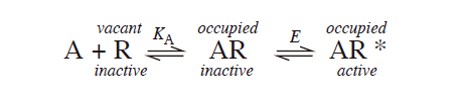 ...................(6)
...................(6)KA: Dissociation equilibrium constant; E: equilibrium constant; A: agonist; R: Receptor (inactive); R*: Receptor (active)
Here, the occupied receptors can exist in inactive (AR) and the other active (AR*) form. Active (AR*) form formation leads to a tissue response. AR and AR* can interconvert (often described as isomerization) and at equilibrium, the receptors will be distributed among the R, AR, and AR* conditions. The position of the equilibrium between AR and AR*, and hence the magnitude of the maximum response of the tissue, will depend on the value of the equilibrium constant E. Suppose that a very large concentration of the agonist A is applied, so that all the binding sites are occupied (i.e., the receptors are in either the AR or the AR* state). If the position of the equilibrium strongly favours AR, with few active (AR*) receptors, the response will be relatively small.
3. Heterotrimeric and Ternary complex model
The heterotrimeric G coupled receptors are involved in a large number of cellular activities and it is one of the main drug targets. The structure of the G-protein is heterotrimeric consisting of three subunits i.e alpha-, beta-, and gamma- subunits. Following activation by GTP binding, the trimer dissociates into its α and βγ subunits, each of which may elicit cell responses.
Previous two models occupancy theory and two state theory doesn't really explain about the tissue response by an agonist that binds to a G-protein coupled receptors (GPCR). The ternary complex model was used to describe ligand, receptor, and G-protein interactions. This model describes a receptor that when activated by an agonist moves laterally in the cell membrane to physically couple to trimeric G protein.
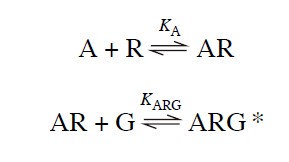
Here, the agonist-receptor complex (AR) combines with a G-protein (G) to form a ternary complex (ARG*), which can initiate further cellular events, such as the activation of adenylate cyclase. However, this simple scheme (the ternary complex model) doesn't consider the importance of isomerization in receptor activation and it also failed to account for mutated receptors. hence, the following equation considers the assumption of receptor activation by isomerization:
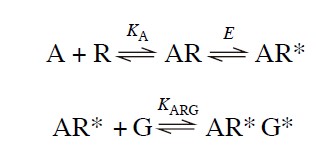
Here, the combination of the activated receptor (AR*) with the G-protein causes the latter to enter an active state (G*) which can initiate a tissue response through, for example, adenylate cyclase, phospholipase C, or the opening or closing of ion channels.
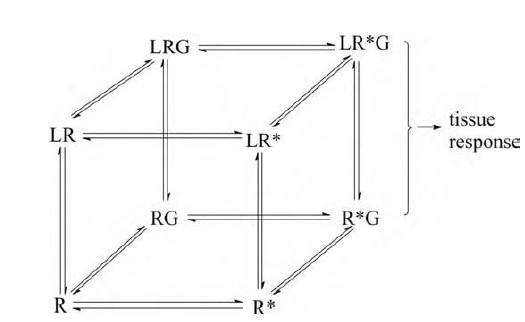
Fig-6: An elaboration of the model reproduced as the front face of the cube.
Each of its four elements (R, R*, LR, and LR*) can combine with a G-protein to form RG, R*G, LRG, and LR*G, respectively. Of these, only R*G and LR*G lead to a tissue response. The top face of the cube shows ligand-bound states of the receptor.
In this scheme, what will determine whether a particular agonist can produce a full or only a limited response? Suppose that a high
concentration of the agonist is applied, so that all the receptors are occupied. They will then be distributed among the AR, AR*, and AR*G* conditions, of which AR*G* alone leads to a response. The values of both E and KARG will then influence how much AR*G* is formed, and hence whether the agonist in question is partial or otherwise. In principle, each of these two equilibrium constants could vary from agonist to agonist.
Suppose that L combines only with the inactive, R, form. Then the presence of L, by promoting the formation of LR at the expense of the other species, will reduce the proportion of receptors in the active, R*, state. L is said to be an inverse agonist or negative antagonist and to possess negative efficacy. If in contrast, L combines with the R* form alone, it will act as a conventional or positive agonist of very high intrinsic efficacy.
4. Operational model
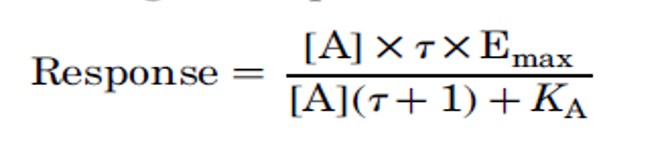
- Emax is the maximal response that can be obtained from the system
- KE the concentration of the AR complex that produces 50% of the maximal response.
- [Rt] is the receptor density
- KA is the equilibrium dissociation constant of the AR complex
- τ (Tau) is the ratio [Rt] / KE
- Changes in the value of τ lead to changes in the responsiveness of the system to agonist, it controls both the potency of the agonist and the maximal response of the agonist.
- An important and versatile parameter in the operational equation is τ;
- This constant incorporates the intrinsic efficacy of the agonist: describing the efficiency of the tissue as it converts agonist-derived stimulus into tissue response
Font Face
Background Colour
Font Size
Text Colour

